
Wiki
Drehstrom
In einem Drehstromnetz gibt es drei energieübertragende Leiter, deren Spannungen um 120° zueinander versetzt sind. Diese drei Spannungen sind ausreichend für die Erzeugung eines kreisförmig rotierenden Magnetfelds durch drei Elektromagnete oder können umgekehrt durch ein rotierendes Magnetfeld erzeugt werden.
Daher lassen sich mit Drehstrom sehr einfach elektrische Netze aufbauen, die von Drehstromgeneratoren gespeist werden und wo durch Drehstrommotoren mechanische Arbeit verrichtet wird. Dabei sind Generatoren und Motoren fast baugleich, weil sie nach dem selben Prinzip funktionieren. Die Vorteile der Drehstrommaschinen (keine Schleifkontakte, hoher Wirkungsgrad, gleichmäßiger Lauf) führten dazu, daß Drehstromnetze weit verbreitet sind.
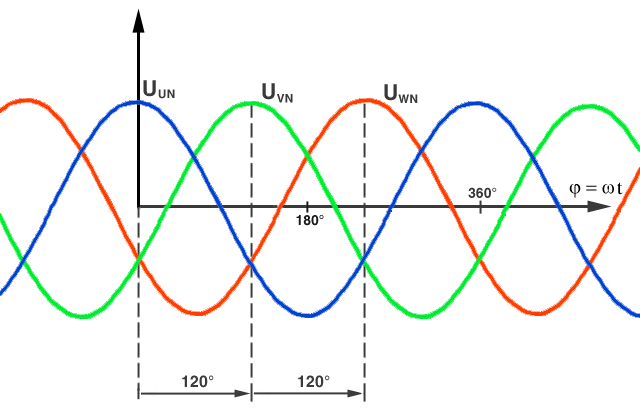
Bild D.1: Die Phasen des Drehstromnetzes als Liniendiagramm
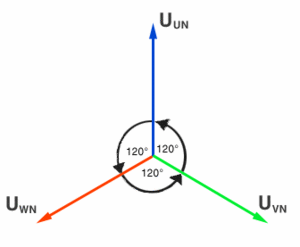
Bild D.2: Die Phasen des Drehstromnetzes als Zeigerdiagramm
Weil die Summe der Spannungen im Drehstromnetz immer gleich Null ist, hat sein Sternpunkt kein Potential gegenüber Erde; wenn die Belastung der einzelnen Phasen jedoch nicht symmetrisch ist, verschiebt sich das Potential des Sternpunkts vom Nullpunkt weg. Man spricht dann von einer Nullpunktverschiebung.
Durch Anschluß an den Neutralleiter kann der Sternpunkt auf Masse gezogen werden, wobei die Schieflast trotz verschwundener Nullpunktverschiebung vorhanden bleibt, aber eine andere Verteilung als vorher aufweist. Der Neutralleiter wird also belastet um das Potential des Sternpunkts auszugleichen. Die maximale Belastbarkeit und das Vorhandensein eines Neutralleiters hängt dabei von der Bauart und Schaltgruppe des Transformators ab.
Mit dem PE-Leiter zusammen hat man also fünf Leiter an einem Drehstromanschluß, wobei der Neutralleiter mit N und die Phasen nach der Phasenfolge mit L1, L2, L3 bezeichnet werden.
Die unterschiedlichen Möglichkeiten der Schaltung der drei Außenleiter an die Last führen zu verschiedenen Schaltgruppen. Eine weitere Unterscheidungsmöglichkeit besteht in dem Drehsinn eines Drehstromanschlusses. Weil man von vielen elektrischen Maschinen eine bestimmte Drehrichtung erwartet, muß häufig zur Sicherheit der Anschluß auf richtige Phasenfolge geprüft werden, obwohl diese eigentlich schon durch die Bezeichnung der Außenleiter und der Anschlüsse des Betriebsmittels vorgegeben ist. Durch Vertauschen zweier beliebiger Phasen kann die Drehrichtung dann gegebenenfalls umgekehrt werden.
Drehstromtransformator
Bei einem D. werden die einzelnen Phasen des Drehstromnetzes magnetisch durch den gemeinsamen Eisenkern verkoppelt. Man könnte auch einen D. aus drei entsprechend verschalteten Einphasentransformatoren (Drehstrombank) aufbauen, aber es ist effizienter das Kernmaterial für alle drei Phasen gleichzeitig zu benutzen. Weil für den magnetischen Fluß das Überlagerungsprinzip gilt, verhält sich der Transformator so, als ob die drei Phasen auf verschiedenen Eisenkernen angebracht wären.
Dieses Verhalten gilt aber nur für idealen Drehstrom; wenn auf Primär- oder Sekundärseite eine Schieflast anliegt, kann die Ausgangsspannung stark abfallen.
Aufbau eines typischen Drehstromtransfromators Schaltgruppe Dyn5
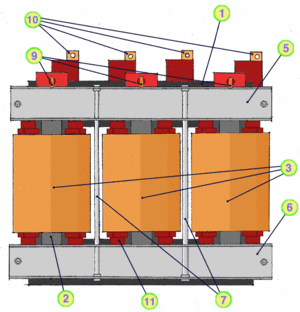
Bild D.4: Drehstromtransformator Dyn5: Oberspannungsseite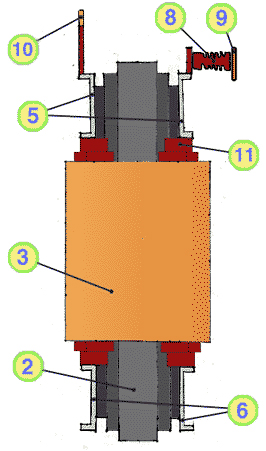
Bild D.5: Drehstromtransformator Dyn5: Seitenansicht
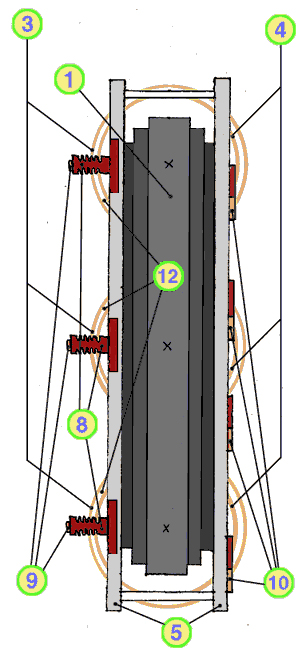
Bild D.6: Drehstromtransformator Dyn5: Ansicht von oben
- Joch des Kerns
- Schenkel des Kerns
- Oberspannungs - Wicklung
- Unterspannungs - Wicklung
- oberes Preßeisen
- unteres Preßeisen
- Zugstangen
- Oberspannungs - Stützer
- Anschlüsse Oberspannung:
U, V, W - Anschlüsse Unterspannung:
U, V, W, N - Abstützklötze
- Streukanal
Die mittlere Wicklung muß nicht so lange Feldlinien erzeugen. Deshalb ist der Leerlaufstrom dort nicht so groß wie an den beiden äußeren Wicklungen.
Außer der abgebildeten Dreischenkel - Bauweise gibt es noch Drehstromtransformatoren mit Fünfschenkelkern, die neben den äußeren Wicklungen noch zwei weitere Schenkel haben und mit einer geringeren Bauhöhe auskommen.
Bezeichnung der Anschlüsse eines Drehstromtransformators
Die Anschlußbezeichnung setzt sich aus drei Teilen zusammen:
- Wicklungsnummer:
Ziffer 1..3
Die Wicklungsnummer unterscheidet nicht die Wicklungsstränge unterschiedlicher Phasen, sondern die meistens galvanisch voneinander getrennten Wicklungen der gleichen Phase, die zusammen auf einem Schenkel des Transformators montiert sind. Üblich sind die Nummern 1 für Oberspannung und 2 für Unterspannung. - Leiteranschluß:
Welcher Leiter soll angeschlossen werden? Für Transformatoren gelten, wie für andere Betriebsmittel auch, die Anschlußbezeichnungen U, V, W, denen bei den Anschlußbezeichnungen des Netzes L1, L2, L3 gegenüberstehen:
U: Außenleiter L1
V: Außenleiter L2
W: Außenleiter L3
N: Neutralleiter - Position innerhalb des Wicklungsstrangs
1: Anfang
2: Ende
3 .. n: Anzapfung zwischen Anfang und Ende, gezählt vom Wicklungsstranganfang aus
Die unterschiedlichen Möglichkeiten die drei Phasen primär- und sekundärseitig zu verschalten werden unter dem Eintrag Schaltgruppen beschrieben.
Berechnung der Bemessungsleistung eines Drehstromtransformators
Bei der Berechnung der Bemessungsleistung aus der Bemessungspannung und dem Bemessungsstrom muß beachtet werden, daß die Spannung eine Außenleiterspannung darstellt und der Strom ein Außenleiterstrom des Transformators ist. Um nun die Bemessungsleistung des Transformators zu bestimmen muß man je nach Schaltgruppe die eine oder die andere dieser beiden Größen auf den entsprechenden Strangwert umrechnen (durch die Wurzel von 3 teilen) und dann das Ergebnis mal drei nehmen (drei Stränge im Drehstromtransformator). Die andere Größe kann so bleiben, weil sie schon dem entsprechenden Strangwert entspricht. Man kommt also immer auf folgendes Ergebnis:![]()
Formel D.1: Bemessungsleistung eines Drehstromtransformators
Siehe auch:
» Kern » Drehstrom » Feldlinien » Leerlaufstrom » Anzapfung » Bemessungsleistung » Bemessungsspannung » Bemessungsstrom » Außenleiterspannung, -stromDrossel
Eine Drossel begrenzt Ströme durch ihre Reaktanz. Zu diesem Zweck wird sie häufig in Reihe vor Verbraucher geschaltet, die einen sehr stark schwankenden Widerstand haben. Es kann dabei auch um die Glättung eines pulsierenden Stroms aus einer Stromquelle gehen.
Bei diesem Anwendungsgebiet spricht man von Glättungsdrosseln (bei der Anwendung auf Gleichstrom: "Gleichstromglättungsdrosseln"). Kommutierungsdrosseln werden in elektronischen Schaltungen als Energiespeicher benötigt.
Drosseln werden je nach Einsatzgebiet völlig unterschiedlich konstruiert, haben aber die gemeinsame Eigenschaft, das es sich um eine einfache Induktivität handelt, die meistens durch eine auf einem Eisenkern aufgebrachte Spule realisiert wird.
Daher kann man sie auch zur Kompensation von Blindlasten, die durch kapazitive Elemente hervorgerufen werden, benutzen. Man bezeichnet sie dann als Kompensationsdrossel. Eine solche Drossel kann auch die Verteilung der Blindleistung in einem Drehstromnetz symmetrieren (d.h. für gleiche Blindlast an allen drei Phasen sorgen). Daher kommt der Name Symmetrierdrossel, der in einem solchen Fall verwendet wird.
Damit sich eine Drossel in Bezug auf Linearität möglichst ähnlich zu einem ohmschen Widerstand verhält, werden meistens Luftspalte in den magnetischen Kreis eingebaut, wodurch der Einfluss der Hysteresekurve des Eisens gesenkt wird. Manchmal ist es sogar sinnvoll, ganz auf den Eisenkern zu verzichten und die Drossel als Luftspule auszulegen.
Eine Schwierigkeit bei der Konstruktion von Drosseln ist, die Erwärmung durch Kupferverluste gering zu halten, wenn sie z.B. in Reihe mit einem Verbraucher betrieben werden.
Dann baut man auch wassergekühlte Drosseln, bei denen das Kühlmittel innen durch den Leiter fließt.
Bei parallel geschalteten Kompensationsdrosseln sind geringe Eisenverluste wichtiger.
Siehe auch:
» Induktivität » Hysteresekurve » EisenverlusteDurchschlagsfestigkeit
Die Durchschlagsfestigkeit eines Isolierstoffs bezeichnet die elektrische Feldstärke, bei der ein plötzlicher Stromfluss einsetzt, weil stark beschleunigte Elektronen den Stoff ionisieren und durchschlagen. Sie wird mit Ed abgekürzt.
Die D. des Isolationsmediums eines Transformators ist mitbestimmend für seine Baugrösse, Lebensdauer und Belastbarkeit.
Bei Trockentransformatoren wird, neben den festen Isolierstoffen der Leiter, Luft als Isolation verwendet. Ihre D. ist abhängig von der Luftfeuchtigkeit und dem Luftdruck. Sie ist außerdem abhängig vom Abstand der Elektroden, bei grösseren Abständen sinkt sie. Deshalb kann man nicht immer dieselbe Feldstärke Ed nehmen und sie mit dem Abstand multiplizieren um die zulässige Spannung zu ermitteln, sondern man muss zuerst anhand einer Tabelle die für den Abstand gültige D. feststellen. In Tabellenwerken wird häufig 1 cm als Abstand für die angegebene Ed (z.B. 21 kV/cm bei Luft) angenommen. Bei festen Isolierstoffen ist es sinnvoller 1 mm als Messtrecke zu wählen, weil bei Messungen im cm - Bereich die Spannung so hoch werden kann, dass es zu einem Überschlag um die Probe herum kommt.
Weil die aus einer angelegten Spannung resultierende maximale Feldstärke von der Form der Elektroden abhängt, reicht die Spannung alleine nicht aus um die Feldstärke zu bestimmen und in Bezug zu der D. zu setzen. Eine geringe Feldstärke bei hoher Spannung erreicht man am besten durch runde, glatte Oberflächen an den betreffenden Leitern. Spitze Ecken führen zu hohen Feldstärken und Glimmentladungen. Daraus kann sich dann leichter ein Lichtbogen bilden.
In Öltransformatoren kann die D. schon durch einen geringen Wasseranteil im Öl stark herabgesetzt werden. Hier spielen auch Teilentladungen eine Rolle, die die Eigenschaften des Öls verschlechtern.
Thermische Alterung ist bei der D. von Öl und festen Isolierstoffen ein wichtiger Aspekt. Sie begrenzt letztendlich die Lebensdauer eines Transformators. Wegen der Erwärmung während des Betriebs wird die D. der Isolation durch Depolymerisation (das Zerbrechen von Molkülketten) und Oxidation herabgesetzt. (siehe Isolierstoffklassen)
Durchschlagsfestigkeit einiger Isolierstoffe
| Stoff | Durchschlagsfestigkeit Ed [kV/mm] |
|---|---|
| Epoxidharz | 35 |
| Glimmer | 25-70 |
| Papier | 5 |
| Polyethylen | 70-100 |
| Porzellan | 35 |
| PVC | 20-35 |
Siehe auch:
» IsolierstoffklassenDurchflutungssatz
Der D. beschreibt die Anordnung und Größe von Magnetfeldern relativ zur Lage und Stärke des felderzeugenden Stroms. In der hier angegebenen Form läßt er sich bei in der Energietechnik üblichen Frequenzen sowohl für gleichbleibende als auch für zeitlich veränderliche Felder anwenden.
Der D. besagt, daß jedes beliebige Umlaufintegral der magnetischen Erregung um eine stromdurchflossene Fläche genau dem Stromfluß durch diese Fläche entspricht.
Das Ergebnis dieses Umlaufintegrals ist eine magnetische Durchflutung , die nicht nur dieselbe Größe, sondern auch dieselbe Einheit (Ampere) wie die Stromstärke hat.
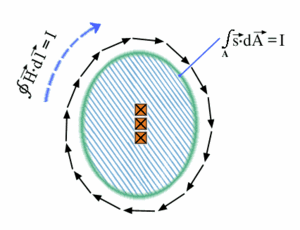
Bild D.7: Der Durchflutungssatz in grafischer Darstellung
Die Stromdichte s ist dabei ein Vektor, der in Richtung des Stromflusses zeigt (das ist in diesem Fall in die Bildebene hinein). Das die Fläche innerhalb des Umlaufintegrals viel größer als der eigentliche Stromleiter ist, spielt keine Rolle. Man kann die Teilflächen, in denen kein Strom fließt einfach ignorieren. Der Oberflächenvektor dA zeigt, wenn man sich entlang des Umlaufvektors dl bewegt senkrecht zur Fläche nach links.
Folgende Formel repräsentiert den D.: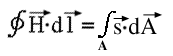
Formel D.2: Der Durchflutungssatz
Zusammen mit der Tatsache, daß für jeden Würfel der hineingehende Fluß gleich dem rausgehenden Fluß ist (Knotenpunktregel; Divergenz von Feldlinien = 0), bildet der Durchflutungssatz die Grundlage für die Berechnung magnetischer Kreise über Widerstandsnetzwerke. Im Unterschied zu dem Strom in Stromkreisen verläuft der magnetische Fluß auch im Vakuum und läßt sich daher nicht exakt auf bestimmte Leiterbahnen eingrenzen. Die genaue Berechnung von Magnetfeldern erfordert deshalb oft die numerische Bestimmung der räumlichen Feldverteilung, die einem sehr komplexen Widerstandsnetzwerk entspricht.
Der Durchflutungssatz ist in dem Sinn eine Analogie zu dem Kirchhoffschen Maschensatz für elektrische Netzwerke, daß die Summe der magnetischen Spannungen genau wie die Summe der elektrischen Spannungen im Stromkreis vorgegeben ist. Der Unterschied ist, daß in der obigen Darstellung des Modells des Magnetkreises die treibende Kraft nicht in dem Kreis sitzt sondern von ihm umschlossen wird. Man kann jedoch die Durchflutung bei der Berechnung von Magnetfeldern mittels eines magnetischen Widerstandsnetzwerks willkürlich an einer bestimmten Stelle in den Magnetkreis als Spannungsquelle einsetzen, vorausgesetzt man beachtet dabei die Verzweigungen, die auftreten.
Dieser Unterschied gegenüber elektrischen Widerstandsnetzwerken liegt also nur in der Betrachtungsweise, die bei Magnetfeldern stark von der räumlichen Feldverteilung geprägt ist und bei ohmschen Netzwerken durch die Aufteilung in unterschiedliche Bauelemente und fest vorgegebene Leiterbahnen bestimmt wird.
Aus den oben beschriebenen Gesetzen folgt, daß sich bei vorgebener Anordnung des Stromleiters über den spezifischen magnetischen Leitwert des Materials, der auch Permeabilität genannt wird, die Flußdichte an jeder Stelle im Raum bestimmen läßt. Das erreicht man bei einem geradlinig in einem homogenen Medium verlaufenden, unendlich langen Stromleiter durch ein kreisförmiges Umlaufintegral, von dem man wegen der Konstanz des Produkts in dem Integral leicht den Betrag der magnetischen Erregung in einer bestimmten Entfernung berechnen kann. Man teilt dazu durch den Umfang des Kreises 2? r und erhält die magnetische Erregung bzw. durch Multiplizieren mit der Permeabilität µ0 µr die magnetische Flußdichte.
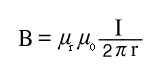
Formel D.3: Flußdichte im Abstand r von einem Leiter mit Strom I
Wenn man den Durchflutungssatz dazu verwendet, um die Verteilung magnetischer Spannungen in einer elektrischen Maschine zu berechnen, muß man beachten, daß sich die ferromagnetischen Abschnitte in dem Kreis wegen der von der Flußdichte abhängigen Permeabilität nichtlinear verhalten. D.h. man kann nur über eine iterative Berechnung auf die Spannungsverteilung kommen; eine Betrachtung als ohmsches Widerstandsnetzwerk reicht nicht aus.
Siehe auch:
» Magnetische Erregung H » Magnetische Durchflutung Θ » Feldlinien » Permeabilität » Magnetische Flußdichte » Hysteresekurve