Wiki

Magnetische Feldlinien geben die magnetische Flußdichte B mit ihrer räumlichen Verteilung wieder. Weil diese Flußdichte eine ortsabhängige, gerichtete Größe ist, kann man eine Feldlinie aus vielen Richtungspfeilen der Flußdichte zusammensetzen, indem man immer wieder ein kleines Stück in der angezeigten Richtung geht und dann neu die Feldrichtung des erreichten Ortes ermittelt.

Das Ergebnis dieses Vorgangs bildet sich von selber aus, wenn man Eisenfeilspäne in ein Magnetfeld gibt. Die Feldlinien werden dann durch die Anordnung der Späne sichtbar.

Das ändert jedoch nichts daran, daß magnetische Feldlinien genau wie Höhenlinien auf einer Landkarte nur ein willkürlich festgelegtes Gedankenmodell sind. Das Magnetfeld ist nämlich stetig im Raum verteilt und konzentriert sich nicht auf bestimmte Linien.

Die ermittelten Feldlinien haben immer die Eigenschaft eine geschlossene Kurve zu bilden und sich gegenseitig nicht zu schneiden. Mathematisch gesehen handelt es sich bei dem Magnetfeld nämlich um ein Vektorfeld, das in allen Punkten die Divergenz 0 hat, d.h. es gibt keine magnetischen Quellen oder Senken in Form eines Monopols, auf den die Feldlinien strahlenförmig zulaufen.
Man stellt Feldlinien häufig so dar, daß ihre Anzahl pro Flächeneinheit einer bestimmten Schnittebene der dort herrschenden Flußdichte entspricht. So kann optisch die Stärke und Richtung des Magnetfelds wiedergeben werden.

Siehe auch:

Als magnetische Flußdichte, magnetische Induktion, magnetische Kraftflußdichte, oder in dem entsprechenden Kontext magnetische Polarisation J bezeichnet man die Dichte der Wirkung des Magnetfelds pro Flächeneinheit. In Formeln wird hierfür ein B verwendet.

Den Betrag dieser Größe kann man sich als abhängig von der Anzahl der Feldlinien pro Flächeneinheit vorstellen.

Formel M.6: Magnetische Flußdichte in Abhängigkeit von magnetischer Erregung und Permeabilität

Die F. gibt aufgrund ihrer Vektornatur Aufschluß über die Stärke und Richtung der magnetischen Einwirkung auf einen bestimmten Ort. Sie wird in der Einheit Vs/m² gemessen, die mit Tesla (T) bezeichnet wird. Früher war die Einheit ein Gauss, was 0,0001 Vs/m² entspricht. Wenn man die F. über eine die Eisenquerschnittsfläche eines Transformators integriert bekommt man den wirkenden magnetischen Fluß als Ergebnis.

Siehe auch:

Der Fluß Φ ist ein Maß, das den Umfang eines Magnetfelds für eine bestimmte Querschnittsfläche wiedergibt. Der Fluß wird in der Einheit Weber (Wb) gemessen, die einem Vs entspricht. Die Ursache für den Fluß ist eine magnetische Durchflutung Θ, die durch den fließenden Strom verursacht wird. Außerdem ist er abhängig von der Permeabilität des Materials, das er durchquert.
Der Fluß durch eine Fläche wird immer durch Integrieren der Flußdichte in Richtung der Oberflächenormalen dA der Fläche errechnet.

D.h. der Fluß einer Fläche bezieht automatisch nur senkrechte Anteile des Magnetfelds mit ein. Das ist bei allen Formeln zu beachten, in denen er vorkommt. Durch folgende Formel werden diese Verhältnisse wiedergegeben: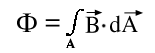

Formel M.5: Definition des magnetischen Flusses

Daher bezieht man sich, wenn man von einem magnetischen Fluß redet, oft unbewußt auf eine dazugehörige Fläche.

Bemerkenswert ist, daß der Fluß durch abgeschlossene Oberflächen von Körpern wie Würfel oder Kugeln immer 0 ist.

Für Bereiche mit konstanter Flußdichte in Richtung der Oberflächennormalen ergibt sich Φ = B *A

Das Induktionsgesetz erklärt den Zusammenhang zwischen zeitlicher Änderung des Flusses und induzierter Spannung.

Siehe auch: