
Wiki
Hysteresekurve
Die Hysteresekurve ist eine für jeden magnetischen Werkstoff spezifische Kennlinie, die die Beziehung von magnetischer Flußdichte B und magnetischer Erregung H im Verlauf eines Ummagnetisierungszyklus darstellt.
Ein Ummagnetisierungszyklus bedeutet stetiger Wechsel von H vom Maximum in eine Richtung zum Maximum in die entgegengesetzte Richtung und wieder zurück.
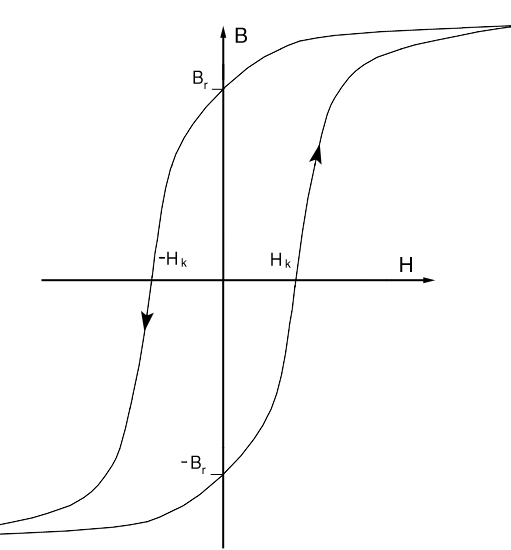
Bild H.1: Hysteresekurve
Man erkennt deutlich, dass wenn der Werkstoff in die Sättigung geht, die magnetische Erregung stark ansteigt, während sich die Flußdichte kaum ändert. Die H. ist mit Pfeilen gekennzeichnet, die angeben, in welcher Richtung sie durchlaufen wird. Die Flußdichte zu einer magnetischen Erregung lässt sich nur bestimmen, wenn bekannt ist ob der Werkstoff gerade aufmagnetisiert oder entmagnetisiert wird.
Man kann eine Neukurve einzeichnen, die den Vorgang des ersten Aufmagnetisierens vom Nullpunkt des Diagramms aus in eine bestimmte Richtung darstellt.
Das Bild zeigt, daß nach der magnetischen Sättigung, wenn der H - Wert wieder sinkt, die Flußdichte nicht so stark abnimmt, wie sie vorher gestiegen ist. Dieser Effekt ist auf die bleibende Ausrichtung der Elementarmagnete in einem ferromagnetischem Werkstoff zurückzuführen. Die Fläche, die sich so innerhalb der H. bildet, ist ein Maß für die Hystereseverluste.
Selbst wenn der Betrag der magnetische Erregung schon auf Null zurückgegangen ist, bleibt aufgrund dieses Effekts noch ein Flußdichte vorhanden. Sie wird als Remanenz Br bezeichnet und kann erst durch eine magnetische Erregung in die andere Richtung, die Koerzitivfeldstärke Hk , auf Null zurückgebracht werden.
Man unterscheidet nach der Form ihrer H. hartmagnetische und weichmagnetische Werkstoffe. Die hartmagnetischen haben eine sehr breite H., d.h. späte, meistens sehr plötzliche Übergänge zur Polarisation in die andere Richtung. Sie haben eine hohe Koerzitivfeldstärke. Weil sich einmal eingeprägte Felder so gut halten, werden diese Werkstoffe zur magnetischen Speicherung von Information verwendet. Die Fläche innerhalb H. ist bei ihnen groß, weshalb sie sich nicht für elektrische Maschinen eignen. Weichmagnetische Werkstoffe haben dagegen eine geringe Koerzitivfeldstärke. Dadurch werden die Fläche innerhalb der H. und damit die Eisenverluste geringer.
Es gibt auch eine andere Darstellungsform der H., bei der die durch eine Spule erzeugte magnetische Feldstärke H der Magnetisierungsfeldstärke M, die durch Polarisation des Materials ensteht, gegenübergestellt wird. Diese H. hat nach Erreichen der Sättigung im Gegensatz zu der hier abgebildeten keine bleibende Steigung µ0 mehr. Die bleibende Steigung entspricht dem üblichen Meßaufbau, wo Strom und integerierte Spannung an einer Spule als Eingangsgrößen für horizontale und vertikale Ablenkung eines Oszilloskops verwendet werden. Die Integration der Spannung kann über einen entsprechend beschalteten Operationsverstärker durchgeführt werden.
Den Zusammenhang zwischen Magnetisierung, Permeabilität und Suszeptibilität erklären die folgenden Formeln: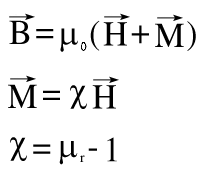
Formeln H.1: Magnetisierung M , relative Permeabilität µr und Suszeptibilität χ
Wobei für ferromagnetische Werkstoffe µr und χ im Verlauf der Kennlinie unterschiedliche Werte annehmen.
Bei der Erfassung einer H. sollte die Zeitverzögerung durch Nachlaufen der Flußdichte gegenüber der magnetischen Erregung keine Rolle spielen. Das heißt, bei dem Meßvorgang wird eine so geringe Frequenz gewählt, daß die Elementarmagnete sich viel schneller ausrichten, als sich das H - Feld ändert. Das bedeutet daß, wenn man an einem Punkt der Kurve anhalten würde (Stromfluß durch die Meßspule plötzlich gleichbleibend), der Meßwert in dem Diagramm auch nach beliebig langer Zeit nicht wegdriften würde.
Die Messung kann also mit einer beliebigen Wellenform durchgeführt werden, solange diese keine zu steilen Sprünge enthält (wie sie bei Rechteck- oder Sägezahnsignalen vorkommen).
Ein weiterer Grund für eine niedrige Meßfrequenz ist, das Meßergebnisse nicht durch von starken Flußdichteänderungen verursachten Wirbelstromverlusten verfälscht werden sollten.
Siehe auch:
» Flussdichte B » Magnetische Erregung H » Hystereseverluste » PermeabilitätHystereseverluste
Hytereseverluste enstehen durch die ständige Umpolung der Elementarmagnete in ferromagnetischen Werkstoffen im wechselnden Magnetfeld. Weil sich die Bereiche gleicher magnetischer Ausrichtung (die Weißschen Bezirke) bei Betragsänderung des Magnetfelds in Richtung Sättigung vergrössern, und dabei unter Aufwendung von Energie ihre Grenzwände neu finden müssen, setzen sie so die Energie des magnetischen Felds in Wärme um.
Die Menge der pro Volumeneinheit verlorenen Energie bei jedem Phasendurchlauf entspricht der Fläche innerhalb der Hysteresekurve. Aus der Formel der investierten elektrischen Energie kann man diese Beziehung über das Induktionsgesetz in Verbraucherschreibweise herleiten:
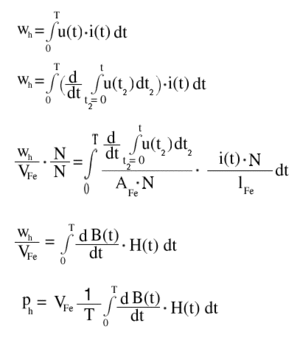
Formel H.2: Herleitung zur Bestimmung der Hystereseverluste
Die obenstehenden Formeln beziehen sich auf die skalaren Größen von B und H, deren Zählpfeile in die selbe Richtung zeigen.
N gibt die Anzahl der Windungen der Meßspule an.
T ist die Dauer einer Schwingunsperiode der Netzfrequenz (T = 1 / f)
VFe, lFe und AFe ergeben sich aus den Abmessungen des magnetischen Kreises:
AFe ist die Querschnittsfläche
lFe ist die mittlere Feldlinienlänge.
VFe = lFe AFe ist das Eisenvolumen, wobei man von einem vollständig mit Eisen gefüllten Kern ausgeht.
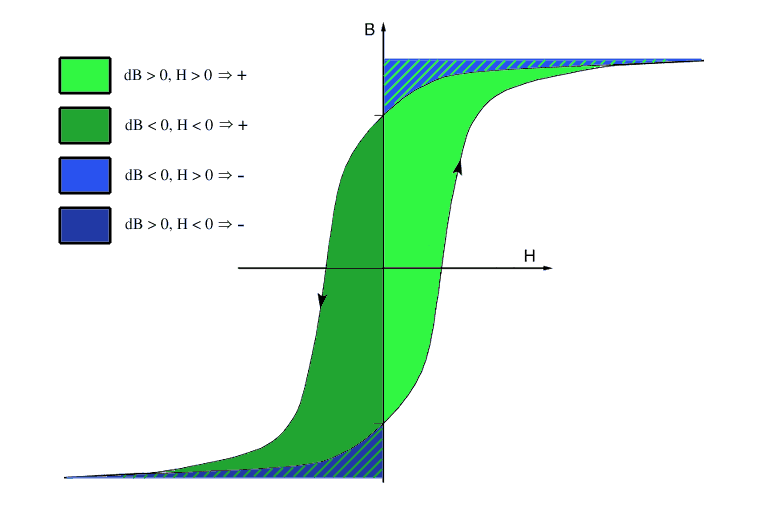
Bild H.2: Anschauliche Darstellung des Integrals
Das Bild zeigt eine grafische Darstellung des Integrals aus Formel H.2.
Die grünen Flächen in dem Bild tragen positiv zu dem Ergebnis bei, die grün - blau gestreiften Abschnitte repräsentieren Überlagerungen von positiven (grünen) und negativen (blauen) Teilflächen, die sich aufheben. Übrig bleibt also nur die Fläche innerhalb der Hysteresekurve.
Die Hystereseverlustleistung steigt daher linear mit der Frequenz und ungefähr quadratisch mit der Flußdichte.
Siehe auch:
» Hysteresekurve » Magnetische Flußdichte