Wiki

Die L. sind die Messgröße, die man erhält, indem man am sekundärseitig unbelasteten Transformator primär die Bemessungsspannung anlegt und dann die aufgenommene Wirkleistung bestimmt. Das Formelzeichen ist P₀.
Die L. bestehen größtenteils aus den Eisenverlusten, so daß man beide gleichsetzen kann.

Der dabei vernachlässigte Anteil sind ohmsche Verluste in den Wicklungen aufgrund des Leerlaufstroms und die Wirbelstromverluste der Wicklungen, die ebenso wie Zusatzverluste am Gehäuse des Transformators, durch das Streufeld des magnetischen Hauptflusses hervorgerufen werden können. Der oberwellenhaltige Leerlaufstrom verursacht über den Streufluß der primären Streuinduktivtät auch Wirbelstromverluste im Kupfer und Zusatzverluste.
Die im vorigen Absatz aufgezählten Wirbelstromverluste und Zusatzverluste müssen jedoch von denen, die den Kurzschlußverlusten zugerechnet werden, unterschieden werden.

Im allgemeinen sind sie so gering, daß sie überhaupt nicht berücksichtigt werden müssen. Nur bei außergewöhnlich streufeldbehafteten Kernformen und großen Leiterquerschnitten spielen sie eine Rolle.

Siehe auch:

Der L. bezeichnet den Strom, der bei anliegender Bemessungsspannung in die Primärseite eines Transformators fließt, während die Sekundärseite unbelastet ist. Er hat das Formelzeichen I₀.

Der hier betrachtete L. bezieht sich auf den eingeschwungenen Zustand. Im Unterschied dazu bezeichnet der Einschaltstrom den Übergang vom unmagnetisierten Transformator zum Leerlaufstrom.

Der Leerlaufstrom hat einen Wirk- und einen Blindanteil. Der Wirkanteil, der Strom der Leerlaufverlustleistung, wird durch die Eisenverluste verursacht, die sich in Hystereseverluste und Wirbelstromverluste aufteilen.

Der Blindanteil ensteht durch die endliche Hauptinduktivität eines realen Transformators (der magnetische Widerstand des Kerns ist nicht 0). Je kleiner eine Induktivität ist, die man an das Netz anschließt, desto größer wird der Blindstrom der fließt. Um die Verluste in den Zuleitungen gering zu halten, versucht man den Leerlaufstrom zu minimieren.

Außerdem kann ein zu hoher Leerlaufstrom das Netz stören, weil reale Netze durch Verbraucher beeinflußt werden können (kein unendlich kleiner Innenwiderstand der Spannungsquelle, Leitungswiderstand nicht 0).
Die Hysteresekurve ist nämlich nicht linear und führt, wenn man sie mit der Sinuswelle der integrierten Eingangspannung verkettet zu einer stark oberwellenhaltigen Stromentnahme, d.h. der Leerlaufstrom ist nicht nur auf die Netzfrequenz beschränkt, sondern enthält Spektralanteile bei den ganzzahligen Vielfachen dieser Frequenz.

Diese zusätzlichen Frequenzanteile können elektronische Verbraucher stören, die oft nur durch das Ausfiltern der 50 Hz - Frequenz vor Beeinflussung geschützt sind. Wegen der Dimensionierung der Netze für eine Stromentnahme, die deutlich über dem L. liegt, kann man die Oberwellen jedoch meistens vernachlässigen.

Die Auswirkungen des Frequenzspektrums des L. auf einen Drehstromtransformator hängen mit von seiner Schaltgruppe ab.
Durch Betrachtung der Sinusfunktionen der Eingangströme kommt man darauf, daß die Ströme der Oberwellen mit einem durch drei teilbaren Vielfachen der Netzfrequenz sich wie eine gleichphasige Belastung verhalten, weil sich die drei Phasen durch Multiplikation des Winkelarguments mit drei immer in der selben Phasenlage befinden (120° x 3 = 360°).

Bei der primärseitigen Schaltgruppe Y führt ein solches Verhalten zu einem unerwünschten Streufeld, bei Schaltgruppe D können die gleichphasigen Anteile des Stroms frei fließen. Vielfache der Netzfrequenz, die nicht durch drei teilbar sind, sind entweder gegenphasig oder verlaufen in der selben Drehrichtung, wie die Eingangspannung, bloß schneller. Diese beiden Fälle sind unproblematisch.

In der Realität kann der L. bei baugleichen Transformatoren um bis zu 30% schwanken, weil schon ein sehr kleiner Luftspalt im Kern den magnetischen Widerstand deutlich erhöht. Geringe Fertigungstoleranzen führen also zu einem großen Unterschied im Leerlaufstrom. Solange der L. im zulässigen Rahmen bleibt resultieren daraus keine negativen Folgen, auch das Übersetzungsverhältnis ändert sich kaum.

Siehe auch:

Die Lenzsche Regel besagt, daß die induzierte Spannung immer die Polarität hat, in der der von ihr verursachte Strom durch sein Magnetfeld der Ursache der Induktion, der Magnetfeldänderung, entgegenwirkt.

Die L. stellt also dar, wie die Physik versucht, den Ist - Zustand aufrecht zu erhalten. Sie ist letztlich eine Sonderform des Energieerhaltungssatz.
Wichtig bei der Anwendung der L. ist die Richtung der Ursache der Induktion richtig festzustellen. Die Ursache einer Induktion ist nämlich immer die Änderung eines Magnetfelds ( Induktionsgesetz). D.h. wenn die Magnetfeldstärke abnimmt, zeigt die Richtung der Ursache genau in entgegengesetzte Richtung zu den Feldlinien. Der induzierte Strom versucht dann das Magnetfeld aufrecht zu erhalten.

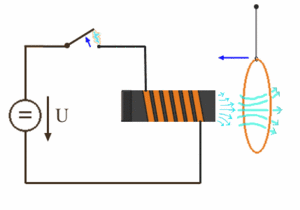
Bild L.1: Anziehung einer frei aufgehängten Leiterschleife beim Abschalten des felderzeugenden Stroms

Die obige Abbildung zeigt, daß die Feldlinien, die in der Leiterschleife durch den induzierten Strom verursacht werden und die Feldlinien, die die felderzeugende Spule während des Abschaltens noch für einen kurzen Augenblick hervorbringt, die gleiche Richtung haben.

Dieses Verhalten führt zu einer Anziehung der Leiterschleife und beruht auf der Stromrichtung des induzierten Stroms, die nach der Lenzschen Regel bestimmt werden kann.

Dabei spielt die Polarität der anliegenden Spannung und der Wickelsinn der Spule keine Rolle; die Leiterschleife wird beim Abschalten immer angezogen.
Die Rechte-Hand-Regel ergänzt die Lenzsche Regel so, daß die Richtungen, die in der L. in Relation zueinander gesehen werden, absolut bestimmt werden können.

Siehe auch:

Die Lorentzkraft ist die Kraft, die von Magnetfeldern auf bewegte elektrische Ladungen ausgeübt wird.

Es ist die folgende grundlegende Beschreibung der Lorentzkraft, die, wo es möglich ist, Begriffe aus der Mechanik (Kraft, Geschwindigkeit) verwendet, üblich:

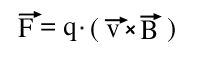
Formel L.1: Kraft F auf Ladung q, die sich mit Geschwindigkeit v durch ein Magnetfeld B bewegt.

Die Lorentzkraft beruht auf der Wechselwirkung des Magnetfelds bewegter Elektronen mit dem Magnetfeld der Umgebung. So ensteht eine Kraft, die freie Elektronen, die sich in einem Magnetfeld senkrecht zu den Feldlinien bewegen, auf eine Kreisbahn zwingt.

Die Richtung der Kraft, die über das Kreuzprodukt in der Formel (das "x") vorgegeben ist, kann auch durch die Rechte-Hand-Regel bestimmt werden.
Wenn man sich eine bewegte Ladung im Magnetfeld vorstellt und um die Ladung herum einen schmalen, unendlich langen Streifen senkrecht zur Bewegungsrichtung herausschneidet, stellt man fest, daß die Änderung des magnetischen Flusses durch die Bewegung der Ladung auf einer Seite größer ist als auf der anderen. Die bewegte Ladung ist nämlich von einem sich vergrößernden und einem immer kleiner werdenden Rechteck auf jeder Seite umgeben. Entlang der Seiten dieser Rechtecke, die sich aus den gerade beschriebenen Streifen zusammensetzen, wird eine Spannung induziert, die die Ladung gemäß der Lorentzkraft ablenkt. Die Lorentzkraft ist also nur eine spezielle Formulierung des Induktionsgesetzes.

Man kann bewegte Ladungen auch als Ströme auffassen. Daher wirkt die L. auch auf die Elektronen eines kontinuierlichen Stromflusses. Dabei ist zu beachten, daß Elektronen eine negative Ladung haben und die technische Stromrichtung der Elektronenbewegungsrichtung entgegengesetzt ist. Also zeigt die technische Stromrichtung letztendlich in Richtung des mit der Ladung q multiplizierten v - Vektors der Formel.

Die Auswirkung der Lorentzkraft auf gegensinnige Stromflüsse, die z.B. innerhalb eines Stromkreises vorkommen, und sich zwangsläufig gegenseitig mit Magnetfeldern durchfluten, ist in der folgenden Darstellung beschrieben:

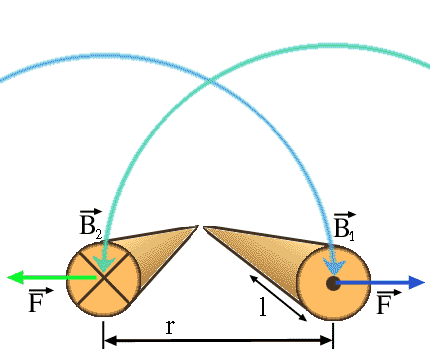
Bild L.2: Lorentzkraft, die zwei Ströme innerhalb eines Streckenabschnitts l auseinanderdrückt.

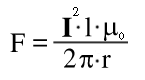
Formel L.2: Kraft auf Abschnitt l zwischen zwei gegensinnigen Strömen I im Abstand r

Die Flußdichte, die dazu dient die Lorentzkraft in diesem Fall zu berechnen, basiert auf dem Durchflutungsatz. In dem Bild wirkt sie in Form einer Streckenlast. Um die Kraft zu bestimmen muß man sich also auf einen Leiterabschnitt einer bestimmten Länge beziehen.

Elektronen in metallischen Leitern können sich zwar innerhalb des Leiters frei bewegen, werden aber daran gehindert den Leiter zu verlassen. Daraus folgt, daß sich eine L. auf den Leiter und das damit verbundene mechanische System überträgt.

Daher ist die L. in elektrischen Maschinen nutzbar. Der durch das magnetische Drehfeld der Ständerwicklung induzierte Strom in einem Kurzschlußläufer ist z.B. immer so gerichtet, daß sie ein gleichmäßiges Drehmoment auf den Läufer ausübt.

Die L. kann, wenn sie unbeabsichtigt auftritt, auch schädliche Auswirkungen haben. In Transformatoren kann sie zu einer mechanischen Zerstörung führen, wenn sie durch einen Blitzeinschlag oder Kurzschluß so schnell ansteigt, daß Schutzeinrichtungen nicht früh genug ansprechen können.

Die Kräfte, die so enstehen, können, falls der Transformator nicht entsprechend ausgelegt ist, bei einem sekundären Kurzschluß einen axialen Schaden verursachen, weil sich die Wicklungen gegenseitig abstoßen und dabei gegen das Joch des Transformators prallen.

Wenn man einen Transformator kurzschlußfest konstruieren will, muß man diese Kräfte durch entsprechende Abstützungen und Verstärkungen auffangen. Ihre Ursache liegt in einem geringfügigen Versatz der Wicklungen gegeneinander aufgrund von Abweichungen in der Wicklungslänge.

Die hier beschriebene Art der Beschädigung ist bei Überspannung nicht so häufig wie die andere Möglichkeit:

Bei einem Kurzschluß oder einer primären Überspannung (z.B. in Folge eines Blitzeinschlags) kann es dazu kommen, daß sich die Wicklungen radial auseinander ziehen. Bei Transformatoren mit eckigen Wicklungen kann das einen Durchbruch der Isolation an den Stellen, wo sie mit dem Kern zusammenstößt, zur folge haben. Durch den hohen Stromfluß können sich sogar die Zuleitungen verbiegen.

Die radiale Ausdehnung der Primärwicklung beruht darauf, daß bei kreisförmigen Strömen die gegenüberliegende Seite eines Punktes auf dem Kreis immer einen Stromfluß in die entgegengesetzte Richtung trägt. Gegenüberliegende Punkte stoßen sich also ab; die Wicklung hat das Bestreben ihren Radius zu vergrößern.

Bei größeren Transformatoren, wo die Primärwicklung immer außen angeordnet ist, wirken diese Zugkräfte nur auf die Primärwicklung; die innenliegende Sekundärwicklung wird zusammengedrückt.

Eine sinnvolle Gegenmaßnahme ist in jedem Fall die Verwendung runder Wicklungen und Kerne, so daß die auftretenden Kräfte keine Biegemomente sondern nur Zug- und Druckkräfte in den Leitern zur Folge haben. Das ist auch ein wichtiger Grund, warum Transformatoren ab einer gewissen Größe zylinderförmige Wicklungen haben.

Die Lorentzkraft hoher Ströme ist deshalb so problematisch, weil sie im Quadrat zur Stromstärke ansteigt.

Siehe auch: